Title: Mathematical Logic Tools and Games

Interactive Games

With interests in mathematical logic, I've curiously downloaded a few theorem provers. However, I have yet to find one with an attractive and usable interface. Joseph Swernofsky told me of his interests in making a theorem proving game. He wants to create an interactive puzzle-like platform that teaches people how use formal logic systems. I'm very interested in working on such projects.

Theorem Enumerators

Previously, I worked on a Propositional Theorem Enumerator. The user feeds in a list of axiom schemes and a positive integer n. We can identify a scheme with the infinite set of formulas that it represents. The program iteratively generates a pairwise non-inclusive covering of all theorems that have an n depth proof.

A proof is a finite list of propositional formulas where each formula matches an axiom scheme or follows from the preceding formulas by modus ponens. Each proof is associated with a labeled rooted tree where the theorem is the root and the axioms are the leaves. The depth of a proof is the height of the associated labeled rooted tree.

A pairwise non-inclusive covering of a set X of propositional formulas is a finite set of propositional schemes Y such that (1) each member of X matches a scheme in Y and (2) no two schemes in Y are related by the inclusion relation on their underlying sets of formulas.

I used the program to quickly verify that some axiomatizations of propositional calculus found here are equivalent. I think it would be interesting to run the program on various finite sets of schemes and attempt to measure the asymptotic growth of the number of schemes in the covering as a function of n. There are two examples below.

The following is a constant growth example. By constant, I mean that after a fixed number of steps there are no new theorems. The significance of this example is that it has constant growth, yet appears to be complicated and challenging to verify by hand.

The following is a linear growth example. We display the covering for theorems with 8 depth proofs. I grouped the theorems to demonstrate the pattern of growth. Notice that we have to reuse the first axiom scheme over and over rather than building theorems from theorems alone.

The Decision Problem

The decision problem for the standard theory of propositional calculus is decidable, that is the problem of deciding if a given formula is a theorem (i.e. a tautology). This problem is coNP-Hard and the best known algorithm that solves it runs in exponential time.

My program can be used to decide the n depth proof problem, that is the problem of deciding if given (f, n) whether the formula f has an n depth proof. This problem is also computationally hard.

Since my program allowed me the vary the axiom schemes and still achieve decidability of the n depth proof problem, I decided to vary the axioms for the decision problem while keeping modus ponens as the only inference rule.

I noticed that each Turing machine can be coded by a finite set of axiom schemes. Therefore, the general decision problem is undecidable, that is the problem of deciding if a given formula can be proven from a given finite list of axiom schemes.

Actually, we will show that each two counter machine can be coded by a finite list of axiom schemes. It is well known that each Turing machine can be simulated by a two counter machine. For an introduction to two counter machines, I refer the reader here.

We will proceed by describing how a two counter machine can be coded by a finite list of axiom schemes. Consider the following recursive sequence of axiom schemes:

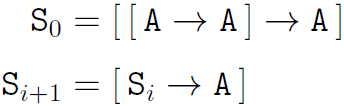
We say that a pair of schemes are disjoint if their underlying sets of formulas are disjoint. One could show that if i and j are distinct, then S_i and S_j are disjoint.

We say that a finite set X of schemes is non-generative if for every scheme T provable from X, there is a scheme in X whose underlying set includes T's underlying set. Intuitively, X is maximal in the sense that it covers all of its own theorems. One could show that if i and j are non-consecutive, then {S_i, S_j} is non-generative.

We refer to the following axiom schemes as configurations because they code configurations for two counter machines. The first value, i, represents the machine's state while the second and third, j and k, represent the machine's counter values.

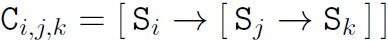
Notice the ordering of the brackets. Although many bracket orderings may work for our construction, each ordering must be treated separately.

Coding transitions is a bit more complicated because whether a configuration matches a transition depends only on the state and whether the counters are empty or not. In other words, there could be infinitely many different configurations that match a single transition. We will need to introduce the following schemes with scheme variable B to store the counter content.

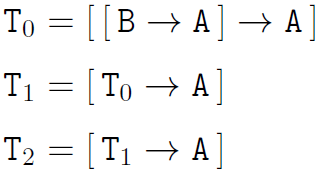
Schemes of the following form will be referred to as transitions:

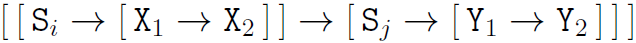
There are a fixed number of values for i and j, one for each state. Then, there are 5 possible cases for X_1 and Y_1 which represent the first counter. Similarly, there are 5 cases for X_2 and Y_2 which represent the second counter.

The 5 cases for the first counter are as follows:

(1) If we want to leave an empty counter unchanged, then X_1 and Y_1 are S_0.
(2) If we want to increment an empty counter, then X_1 is S_0 and Y_1 is S_1.
(3) If we want to leave a non-empty counter unchanged, then X_1 and Y_1 are T_1.
(4) If we want to increment a non-empty counter, then X_1 is T_1 and Y_1 is T_2.
(5) If we want to decrement a non-empty counter, then X_1 is T_1 and Y_1 is T_0.

When referring to T_0, T_1, and T_2 for the second counter, we will actually need to use a different scheme variable in place of B so that both the first and second counter content can be distinct.

One can now represent a two counter machine by taking the associated initial configuration and the associated transitions. I claim that any finite set of configurations and transitions is non-generative, unless there is a configuration and a transition that match. It follows that one can simulate any two counter machine with a finite list of axiom schemes.

I challenge the reader to rigorously prove the preceding claim. One must split into several cases and carefully analyze the tree structure of the propositional schemes to show that particular pairs of schemes are non-generative.